B+Tree 검색, 삽입, 삭제
B+Tree의 검색, 삽입, 삭제에 대해서 알아보도록 하겠습니다
B+Tree를 모른다면 아래의 링크를 참고하세요 또한 B-Tree의 검색, 삽입, 삭제를 보고 오시기 바랍니다.
B-Tree 검색, 삽입, 삭제
B-Tree의 검색, 삽입, 삭제에 대해 알아보고자 합니다 B-Tree에 대해 모르신다면 아래의 링크를 보고 오시면 좋을 것 같습니다. https://junuuu.tistory.com/13 B-Tree 와 B+Tree B-Tree란? 데이터베이스와 파일..
junuuu.tistory.com
B-Tree 와 B+Tree
B-Tree란? 데이터베이스와 파일 시스템에서 널리 사용되는 트리 자료구조의 일종으로 , 이진트리를 확장해 하나의 노드가 가질 수 있는 자식 노드의 최대 숫자가 2보다 큰 트리 구조입니다. 많은
junuuu.tistory.com
또한 검색, 삽입, 삭제를 처음 공부하신다면 아래의 링크에서 직접 데이터를 추가, 삭제하면서 같이 보면 이
해하는데 큰 도움이 됩니다(대신 아래 예제랑은 분할되는 범위가 조금 다를 수 있습니다.)
https://www.cs.usfca.edu/~galles/visualization/BPlusTree.html
B+ Tree Visualization
www.cs.usfca.edu
B-Tree와 유사하지만 B+Tree는 조금씩 다른데 B-Tree는 오른쪽 자식으로 자신보다 큰값을 가지지만 B+Tree는 같거나 큰 값을 가진다. 또한 모든 데이터가 leaf node에 순차적으로 연결된 구조를 가지는 차이점이 있다.
검색(Search)
1. k 값이 Tree에 존재하는지 확인하기 위해 root node부터 탐색을 시작한다.
2. node를 검사하며 작으면 왼쪽자식으로 크거나 같으면 오른쪽 자식으로 이동한다.
3. 이때 항상 leaf node 에서 k 값이 발견되어야 한다.
다음 그림은 3-way B+Tree 에서 7 값을 검색하는 과정입니다

다음 그림은 4-way B+Tree 에서 16값을 검색하는 과정입니다.
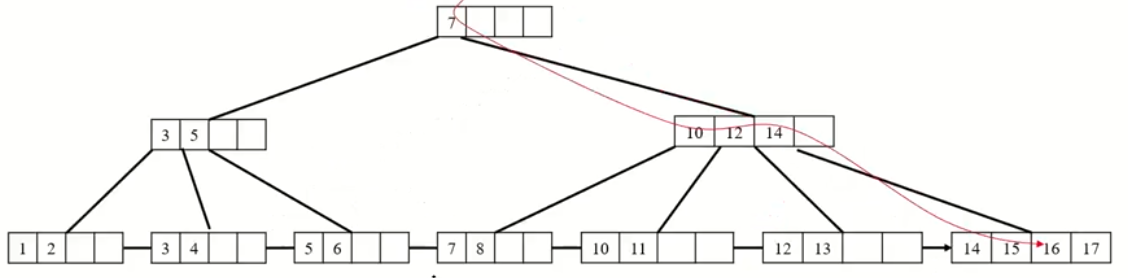
삽입(Insert)
1. k가 들어갈 leaf node T를 찾습니다.
2. k 값을 넣고 MAX_KEY 조건을 위배하는지 검사합니다.
3. 조건을 위배하지 않는다면 종료하고, 조건을 위배한다면
이때 []은 ceiling 함수를 뜻합니다. [2.5] = 3
Left : 0 to [(m-1) /2 ] -1
Middle : [(m-1) /2]
Right [(m-1) /2 ] to m-1
Middle은 부모로 Left는 왼쪽자식 Right는 오른쪽 자식으로 재구성하게 됩니다.
이후에 T=Middle으로 하고 다시 2번으로 돌아가서 T가 MAX_KEY 조건을 위배하는지 검사하게 됩니다.
MAX_KEY 조건 = m-way b+tree일때 key값이 m-1개를 초과하면 발생하게 됨
B-Tree와 어떤것이 다를까요?
Left, Middle, Right를 구분하는 범위가 다릅니다. 왜냐하면 3-way B+Tree에서 [1, 2, 3]이 MAX_KEY 조건을 위배해서 쪼개진다고 하면 원래는 1 LEFT , 2 MIDDLE, 3 RIGHT로 쪼개지지만 B+Tree에서는 그렇게 되면 leaf node 부분에서 2라는 값이 날아가기 때문에 Left 1, Middle 2, Right 2, 3으로 쪼개져야 합니다.
6-way B+Tree로 예제를 살펴보겠습니다.
아래그림과 같이 1,2,3,4,5가 Root 노드에 있다고 생각해 보겠습니다.
그리고 여기에 k값 6을 넣어보도록 하겠습니다.

1. 6이 들어갈 leaf node T를 찾습니다. ( 여기서는 leaf node T는 1, 2, 3, 4, 5입니다)
2. k 값을 넣고 MAX_KEY 조건을 위배하는지 검사합니다. (T에 6을 넣으면 값이 6개로 MAX_KEY 조건을 위배합니다.)
3. 조건을 위배하지 않는다면 종료하고, 조건을 위배한다면
Left : 0 to 2
Middle : 3
Right 3 to 5
Middle은 부모로 Left는 왼쪽 자식 Right는 오른쪽 자식으로 재구성하게 됩니다.
이후에 T=Middle으로 하고 다시 2번으로 돌아가서 T가 MAX_KEY 조건을 위배하는지 검사하게 됩니다.
여기서는 Middle은 3으로 위배하지 않습니다.
다음 그림은 6이 삽입된 후 트리입니다.

여기서 순차적으로 20까지 넣게 되면 트리의 모습은 아래와 같습니다

그러면 여기서 21을 넣으면 어떻게 될까요?
1. 21이 들어갈 leaf node T를 찾습니다. ( 여기서는 leaf node T는 16, 17, 18, 19, 20입니다)
2. k 값을 넣고 MAX_KEY 조건을 위배하는지 검사합니다. (T에 21을 넣으면 값이 6개로 MAX_KEY 조건을 위배합니다.)
3. MAX_KEY 조건을 위배하지 않는다면 종료하고, 위배한다면 트리의 재구성이 일어납니다.
Left16, 17, 18
Middle19
Right19, 20, 21
Middle은 부모로 Left는 왼쪽 자식으로 Right는 오른쪽 자식으로 트리가 재구성됩니다
4. T를 Middle(부모)로 놓고 다시 2번으로 돌아가 MAX_KEY 조건을 위배하는지 검사합니다. ( T에 19가 올라가기 때문에 값이 6개로 MAX_KEY 조건을 위배합니다.)
5. MAX_KEY 조건을 위배하지 않는다면 종료하고, 위배한다면 트리의 재구성이 일어납니다. (부모에서 재구성이 일어날 때는 B-Tree처럼 발생하게 됩니다) = (left node 가 아니라면)
이때 []는 floor 함수 [1.9] = 1
Left 0 to [m-1 /2 ] -1
Middle [m-1 / 2 ]
Right [m-1 /2 ] +1 to m-1
Left 4, 7
Middle 10
Right 13, 16, 19
Middle은 부모로 Left는 왼쪽 자식으로 Right는 오른쪽 자식으로 트리가 재구성됩니다.
6. T를 Middle(부모로)로 놓고 다시 2번으로 돌아가 MAX_KEY 조건을 위배하는지 검사합니다. ( T는 13이 올라가고 값이 1개로 MAX_KEY 조건을 위배하지 않습니다.)
7. MAX_KEY 조건을 위배하지 않아서 종료하게 됩니다. 만약 위배했다면 트리의 재구성이 다시 발생하게 됩니다.
다음 그림은 21이 삽입된 후 트리입니다(visualization의 경우 left가 3개 midle1개 right2개로 쪼개집니다)

B-tree와 다르게 B+tree 에서는 leaf node와 internal node와 분할과정에서 left, right, middle을 나눌 때 범위가 다릅니다!
다음과 같은 5-way B+tree 그림에서 3을 넣으려면 어떻게 해야 할까요?

1. k 값을 넣은 leaf node T를 찾습니다. ( 여기서 T는 0, 1, 2, 5)입니다
2. T에 k값을 넣고 MAX_KEY 조건을 위배하는지 검사합니다. (node T의 0, 1, 2, 3, 5로 key의 값이 5개여서 MAX_KEY 조건을 위배합니다. )
3. MAX_KEY 조건을 위배했으므로 분할이 발생합니다.(leaf node에서 분할 발생)
이때 []은 ceiling 함수를 뜻합니다. [2.5] = 3
Left : 0 to [(m-1) /2 ] -1
Middle : [(m-1) /2]
Right [(m-1) /2 ] to m-1
Left 0, 1
Middle 2
Right 2, 3, 5
Middle은 부모로 올라가고 Left는 왼쪽 자식 Right는 오른쪽 자식으로 재구성됩니다.
Middle을 T로 놓고 다시 MAX_KEY 조건을 위배하는지 검사합니다.(node T는 2, 10, 20, 30, 40으로 key의 값이 5개여서 MAX_KEY 조건을 위배합니다.)
4. MAX_KEY 조건을 위배했으므로 분할이 발생합니다. (internal node에서 분할 발생)
이때 []는 floor 함수 [1.9] = 1
Left 0 to [m-1 /2 ] -1
Middle [m-1 / 2 ]
Right [m-1 /2 ] +1 to m-1
Left 2, 10
Middle 20
Right 30, 40
Middle은 부모로 올라가고 Left는 왼쪽 자식 Right는 오른쪽 자식으로 재구성됩니다.
Middle을 T로 놓고 다시 MAX_KEY 조건을 위배하는지 검사합니다. (node T는 20으로 key의 값이 1개여서 MAX_KEY 조건을 위배하지 않습니다.) -> 따라서 종료하게 됩니다.
다음 그림은 3을 넣은 후 tree 모습입니다.

삭제(Delete)
삭제에서는 어떤 값을 계속하기 때문에 삽입과 반대로 MIN_KEY 조건이 들어가게 됩니다. (삽입은 MAX_KEY 조건)
root node는 최소 1개 이상의 key를 가지고 그 외에는 최소 [m / 2 ] -1 개의 key를 가짐
이때 []는 ceiling 함수 = 천장 함수, [2.5] = 3
3-way에서는 1개의 key를 가져야 함
4-way에서는 1개의 key를 가져야 함
5-way에서는 2개의 key를 가져야 함
6-way에서는 2개의 key를 가져야 함
B-tree에서 삭제를 보고 오셨다고 가정하고 바로 예제로 들어가 보도록 하겠습니다
여기서 B-tree와의 차이점은 B-tree는 internal node에서도 삭제가 발생하지만 B+tree는 leaf node에서만 삭제가 발생합니다!
다음과 같은 5-way B+tree에서 65를 삭제하려면 어떻게 해야 할까요?

1. k 값을 가진 leaf node T를 탐색합니다 (여기서 T는 40, 65, 70입니다)
2. T에서 k값을 삭제하고 MIN_KEY 조건을 위배하는지 확인합니다. (key는 40, 70으로 2개로 MIN_KEY 조건을 위배하지 않습니다.)
3. MIN_KEY 조건을 위배하지 않아 종료합니다.
다음 그림은 65를 삭제한 후 tree입니다.

그러면 다음 그림에서 40을 지우면 어떻게 될까요?

1. k 값을 가진 leaf node T를 탐색합니다 (여기서 T는 40, 65, 70입니다)
2. T 에서 k값을 삭제하고 MIN_KEY 조건을 위배하는지 확인합니다. (key는 65, 70으로 2개로 MIN_KEY 조건을 위배하지 않습니다.)
3. MIN_KEY 조건을 위배하지 않습니다. 그러면 종료해야 하지만 이대로 끝날까요?
4. B+tree에서는 맨 왼쪽 값의 key를 삭제했기 때문에 부모 노드의 40 값을 65로 바꿔줘야 합니다.
다음 그림은 40을 삭제한 후 tree입니다

그러면 다음 그림에서 17을 삭제하면 어떻게 될까요?

1. k 값을 가진 leaf node T를 탐색합니다 (여기서 T는 17, 18, 20입니다)
2. T에서 k값을 삭제하고 MIN_KEY 조건을 위배하는지 확인합니다. (key는 18, 19로 2개로 MIN_KEY 조건을 위배하지 않습니다.)
3. MIN_KEY 조건을 위배하지 않습니다. 그러면 종료해야 하지만 이대로 끝날까요?
4. B+tree에서 맨 왼쪽 값의 key를 삭제했기 때문에 부모로 recursive 하게 올라가서 root node의 17을 18로 update 해야 합니다.
다음 그림은 18을 삭제한 후 tree입니다

그러면 다음 그림에서 30을 삭제하면 어떻게 될까요?

1. k 값을 가진 leaf node T를 탐색합니다 (여기서 T는 25, 30입니다)
2. T에서 k값을 삭제하고 MIN_KEY 조건을 위배하는지 확인합니다. (key는 25로 1개로 MIN_KEY 조건을 위배합니다.)
3. MIN_KEY 조건을 위배했으므로 B-tree와 유사하게 왼쪽이나 오른쪽에서 빌려와야 합니다.
4. LS(Left Sibiling) 왼쪽 자식에서 값을 빌려올 수 있으니 20을 빌려옵니다. 이때 B-tree랑 다른 점은 B-tree는 LS에서 빌려온 값이 부모로 올라가고 부모의 값이 T로 내려가는 구조지만, B+tree는 부모의 값이 T로 내려가지 않고 LS의 값이 부모와 T의 값으로 대체됩니다.
다음 그림은 30이 삭제된 후 tree입니다. ( LS(17, 18, 20)에서 20은 지워져야 합니다)

다음 그림에서 20을 지우면 어떻게 될까요?

1. k 값을 가진 leaf node T를 탐색합니다 (여기서 T는 17, 20입니다)
2. T에서 k값을 삭제하고 MIN_KEY 조건을 위배하는지 확인합니다. (key는 17로 1개로 MIN_KEY 조건을 위배합니다.)
3. MIN_KEY 조건을 위배했으므로 B-tree와 유사하게 왼쪽이나 오른쪽에서 빌려와야 합니다. (왼쪽에서 빌려올 수 없으므로 오른쪽에서 빌려와야 합니다)
4. RS(오른쪽 자식)에서 빌려와도 MIN_KEY 조건을 위배하지 않아서 빌려올 수 있습니다. 가장 작은 값인 25를 빌려오는데 이때 부모도 25 값을 가지고 있기 때문에 부모 노드의 25는 27로 업데이트될 것입니다.
다음 그림은 20이 삭제된 후 tree입니다.

그러면 다음 그림에서 7을 삭제하려면 어떻게 해야 할까요?

1. k 값을 가진 leaf node T를 탐색합니다 (여기서 T는 7, 15입니다)
2. T에서 k값을 삭제하고 MIN_KEY 조건을 위배하는지 확인합니다. (key는 15로 1개로 MIN_KEY 조건을 위배합니다.)
3. 우선 맨 왼쪽 값을 삭제했기 때문에 부모 노드의 7이 삭제되고 15로 업데이트됩니다.
4. 그 후 MIN_KEY 조건을 위배했으므로 B-tree와 유사하게 왼쪽이나 오른쪽에서 빌려와야 합니다. (왼쪽, 오른쪽 둘 다에서 빌려올 수 없는 상황입니다 = 빌려오게 되면 LS, RS에서 MIN_KEY 조건을 위배하게 됩니다)
5. 그렇게 되면 왼쪽 또는 오른쪽으로 merge 해야 하는 상황입니다.

6. LS, PLV, T를 merge 합니다 0, 5, 15가 PRV의 왼쪽 자식으로 되고 T를 P로 변경한 후 MIN_KEY 조건을 위배하는지 확인합니다. P는 25로 key 값이 1개이기 때문에 MIN_KEY 조건을 위배합니다.
7. LS는 존재하지 않고 없고 RS의 key 값은 65, 75, 85로 3개이기 때문에 RS에서 빌려올 수 있습니다.
8. T는 leaf node가 아니기 때문에 일반적인 b-tree처럼 merge가 발생합니다 부모의 35가 T로 내려오게 되고 부모로 RS의 65가 올라가게 됩니다.
9. 부모를 다시 T(65)로 두고 MIN_KEY 조건을 검사하고 root node는 최소 1개의 키만 가지면 되기 때문에 MIN_KEY 조건을 위배하지 않습니다.
7을 삭제한 후 tree입니다

그러면 위의 그림에서 37을 삭제하면 어떻게 될까요?
1. k 값을 가진 leaf node T를 탐색합니다 (여기서 T는 35, 37입니다)
2. T에서 k값을 삭제하고 MIN_KEY 조건을 위배하는지 확인합니다. (key는 35로 1개로 MIN_KEY 조건을 위배합니다.)
3. 맨 왼쪽 값을 삭제하지 않았으니 부모는 업데이트하지 않습니다
4. MIN_KEY 조건을 위배했으므로 LS 또는 RS에서 값을 빌려와야 하는데 RS는 존재하지 않고 LS(25, 30)으로 값을 빌려오게 되면 값이 1개로 MIN_KEY 조건을 위배하기 때문에 빌려올 수 없습니다. ( 5- way B+tree 에서 MIN_KEY 조건은 2개)
5. 왼쪽 또는 오른쪽으로 merge 해야 하고 왼쪽으로 merge를 진행합니다.

6. 부모 노드 25의 오른쪽 자식으로 25, 30, 35로 합쳐지게 되고 부모 노드를 T로 놓고 MIN_KEY 조건을 위배하는지 검사합니다
7. 부모 노드는 25의 값을 1개 가지기 때문에 MIN_KEY 조건을 위배하므로 LS 또는 RS에서 값을 빌려와야 합니다( 하지만 LS는 존재하지 않고 RS(75, 85)에서는 값을 빌려올 수 없는 상황입니다.)
8. LS 또는 RS에서 값을 빌려올 수 없으므로 T, P, RS가 merge 됩니다.
9. P가 다시 T 가 되고 MIN_KEY 조건을 위배하지 않기 때문에 종료하게 됩니다
다음은 37이 삭제된 후 tree입니다
