-
B-Tree 검색, 삽입, 삭제CS/데이터베이스 2021. 11. 15. 18:58반응형
B-Tree의 검색, 삽입, 삭제에 대해 알아보고자 합니다
B-Tree에 대해 모르신다면 아래의 링크를 보고 오시면 좋을 것 같습니다.
B-Tree 와 B+Tree
B-Tree란? 데이터베이스와 파일 시스템에서 널리 사용되는 트리 자료구조의 일종으로 , 이진트리를 확장해 하나의 노드가 가질 수 있는 자식 노드의 최대 숫자가 2보다 큰 트리 구조입니다. 많은
junuuu.tistory.com
또한 검색, 삽입, 삭제를 처음 공부하신다면 아래의 링크에서 직접 데이터를 추가, 삭제하면서 같이 보면 이해하는데 큰 도움이 됩니다.
https://www.cs.usfca.edu/~galles/visualization/BTree.html
B-Tree Visualization
www.cs.usfca.edu
다음 그림은 5차 B-Tree, 5-way B-Tree의 그림입니다.

검색(Search)
일반적인 트리 탐색과 같습니다 어떤 요소 K를 검색할 때 그 요소보다 작으면 왼쪽으로 요소보다 크면 오른쪽으로 이동을 하며 탐색을 합니다.
14를 검색한다고 가정해보겠습니다. 루트부터 시작해서 검색을 시작합니다 3보다 크고, 8보다 크고, 12보다 크고 15보다 작으므로 12와 15 사이에서 연결된 노드로 이동하게 됩니다. 이동후에 다음 노드에서 13보다 크기 때문에 오른쪽으로 이동하는데 그 값이 14와 이므로 탐색하게 됩니다
4를 검색한다고 가정해보겠습니다. 루트부터 시작해서 검색을 시작합니다. 3보다 크고, 8보다 작기 때문에 3과 8 사이에 연결된 노드로 이동하게 됩니다. 이동후에 다시 처음 요소부터 검사를 시작하게 되고 처음 요소가 4이기 때문에 탐색을 끝내게 됩니다.
18을 검색한다고 가정해보겠습니다. 루트부터 시작해서 3보다 크고, 8보다 크고, 12보다 크고, 15보다 크므로 가장 오른쪽에 연결된 노드로 이동하게 됩니다. 이동후에 처음 요소부터 검사를 시작하게 되고 16보다 크고, 17보다 크고 모든 요소의 값을 불렀고 17 오른쪽에 연결되어 있는 노드가 없기 때문에 18은 트리에 존재하지 않는다고 판단하게 됩니다.
(null을 반환하든, print(not found)를 하던)
삽입(Insert)
1. k를 넣을 leaf node T를 찾습니다.
2. T가 MAX_KEY 조건을 어기지 않았다면 끝나게 됨 ( MAX_KEY 조건이란 M-way 트리에서 최대 m-1개의 key를 가질 수 있음을 의미합니다)
3. 만약에 T가 MAX_KEY 조건을 어겼다면 ( M-way 트리에서 key가 m개가 되었다면?) 3 부분으로 나뉘어야 함
이때 []는 floor함수 = 바닥 함수 , [2.5] = 2
Left : 0 to [(m-1)/2] -1
Middle : [(m-1)/2]
Right : [(m-1)/2] +1 to m-1
이렇게 나눈 부분들로 Middle은 부모 노드가 되고, Left는 왼쪽 자식, Right는 오른쪽 자식으로 만들어 나갑니다.
그 이후에 Middle 노드(부모 노드)를 T로 만들고 2번을 다시 수행합니다.
2번으로 돌아가는 이유? Middle이 부모 노드로 올라가기 때문에 부모 노드가 MAX_KEY 조건을 어기는지 확인할 필요가 있음 그래서 조건을 어기지 않는다면 끝나게 됨
6-way B-tree로 예제를 살펴보겠습니다
아래와 같이 1,2,3,4,5가 Root 노드에 있다고 생각해 보겠습니다.
그리고 여기에 k값인 6을 넣어보도록 하겠습니다

현재 Tree 1. 6을 넣을 leaf node T를 찾습니다
2. leaf node T는 1, 2, 3, 4, 5, 6 이 됩니다. 이때 6-way 트리에서 MAX_KEY는 m-1 = (6-1)으로 5개입니다.
3. MAX_KEY 조건을 어겼으므로 3 분할이 시작됩니다.
Left : 0 to 1
Middle : 2
Right : 3 to 5
Middle은 부모 노드가 되고, Left는 왼쪽 자식, Right는 오른쪽 자식이 됩니다
이후 부모 노드로 MAX_KEY 조건을 어겼는지 확인해 봤을 때 Middle은 3을 하나 가지기 때문에 어기지 않았으므로 종료하게 됩니다.
아래의 그림은 6이 들어온 후 상태입니다.

6이 들어온 후 Tree 아래 그림은 이후에 key를 계속 순차적으로 삽입하여 20까지 삽입했을 때의 Tree입니다

순차적으로 20까지 삽입한 후 Tree 그리고 여기에 k값인 21을 넣어보도록 하겠습니다
1. 21을 넣을 leaf Node T를 찾습니다 ( root에서 21을 탐색했을 때 가장 오른쪽 연결로 이동하여야 하며 해당 노드( 가장 오른쪽 연결로 이동한 노드)가 leaf Node이므로 16, 17, 18, 19, 20을 가지고 있는 노드가 T가 됩니다.
2. 21을 값을 넣어주게 되면 16, 17, 18, 19, 20, 21이 되며 MAX_KEY 조건을 어기게 됩니다
3. MAX_KEY 조건을 어겼으므로 3 분할이 시작됩니다.
Left : 0016, 0017
Middle : 0018
RIGHT : 0019, 0020, 0021
Middle은 부모로 가게 되고, Left는 왼쪽 자식, Right는 오른쪽 자식으로 분할됩니다.
이때 부모 노드가 T가 되고 다시 MAX_KEY 조건을 위배했는지 검사하며 부모 노드 T는 3, 6, 9, 12, 15, 18으로 MAX_KEY 조건을 위배하게 됩니다. 다시 3 분할이 시작됩니다.
Left : 0003, 0006
Middle : 0009
RIGHT : 0012, 0015, 0018
Middle은 부모로 가게 되고, Left는 왼쪽 자식, Right는 오른쪽 자식으로 분할됩니다.
다시 부모 노드는 T가 되고 MAX_KEY 조건을 위배했는지 검사하며 부모 노드 T는 9로 MAX_KEY 조건을 위배하지 않았으므로 끝나게 됩니다.
아래 그림은 21을 삽입한 후 Tree입니다.

21을 삽인한 후 Tree 삭제(Delete)
삭제에서는 어떤 값을 계속하기 때문에 삽입과 반대로 MIN_KEY 조건이 들어가게 됩니다. (삽입은 MAX_KEY 조건)
root node는 최소 1개 이상의 key를 가지고 그 외에는 최소 [m / 2 ] -1 개의 key를 가짐
이때 []는 ceiling 함수 = 천장 함수, [2.5] = 3
3-way에서는 1개의 key를 가져야 함
4-way에서는 1개의 key를 가져야 함
5-way에서는 2개의 key를 가져야 함
6-way에서는 2개의 key를 가져야 함
삭제하기 전에 아래 그림처럼 변수를 지정하고 가겠습니다(나중에 삭제할 때 쓰기 위해)
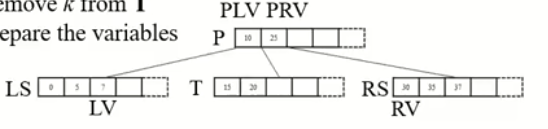
T는 k값을 가지고 있는 노드라고 했을 때, T보다 작은 부모 값을 부모 값을 PLV, T보다 큰 부모 값을 PRV, 그 부모 노드는 P, T의 LS(Left Sibling)의 가장 큰 수를 LV, T의 RS(Right Silbing)의 가장 작은 수를 RV라고 하도록 하겠습니다.
1. 삭제할 k가 포함된 node T를 탐색합니다.
2. node T가 leaf node일 때와 아닐 때가 구분됩니다.
3. leaf node일 때
3-1 node T에서 k를 지운다. 이때 MIN_KEY 조건을 위배하지 않는다면 끝나게 되고
MIN_KEY 조건을 위배한다면 왼쪽(LS)에서 빌려올 수 있다면 왼쪽에서 빌려와서 LV, PLV, T로 트리를 재조합
만약 왼쪽(LS)에서 빌려올 수 없다면 오른쪽(RS)에서 빌려와서 T, PRV, RV로 트리를 재조합한다.
그런데 RS, LS 둘 다에서 빌려올 수 없다면 어떻게 해야 할까?
빌려 올 수 없다는 의미는 LS, RS에서 빌려주게 되면 LS, RS도 MIN_KEY 조건을 위배하는 경우이다.
그런 경우에는 LS와 RS 둘 중 하나를 선택해서 합쳐버리면 된다.
LS, PLV, T를 합쳐서 P의 왼쪽 자식으로 또는 T, PRV, RV를 합쳐서 P의 오른쪽 자식으로 만드는 것이다.
이 경우 P의 값을 하나 가져와서 자식으로 내리기 때문에 P가 MIN_KEY 조건을 위배할 수 있는 상황이 발생했다.
그렇기 때문에 T를 P로 놓고 다시 MIN_KEY 조건을 위배하는지 검사해야 한다.
4. T가 internal node 일 때
삭제하기 전 아래 그림처럼 변수를 지정하고 가겠습니다(나중에 삭제할 때 쓰기 위해)

k는 삭제해야 할 값이라고 하면 LC는 왼쪽 자식, RC는 오른쪽 자식이며 LV는 LC에서 가장 큰 값, RV는 RC에서 가장 작은 값입니다.
4-1 node T에서 k값을 제거하게 되면 LC, RC가 붕뜨게 되므로 k값을 대체할만한 값을 채워 넣어야 합니다.
그 값으로 적당한 게 LV 또는 RV가 될 것입니다.(k의 직전수, 직후수 이기 때문에) 이때 그러면 LV나 RV를 뽑아올 예정이므로 LC나 RC에서 MIN_KEY 조건을 위배할 수 있는 상황이 발생하겠죠? 따라서 LC가 MIN_KEY 조건을 위배하지 않는다면 LV를 뽑아오고, LC는 뽑아왔을 때 MIN_KEY 조건을 위배한다면 RC에서 MIN_KEY 조건을 확인하고 뽑아올 수 있다. 만약 위배한다면 뽑아올 수 없다.
그러면 LC, RC에서 둘 다 빌려올 수 없다면 어떻게 해야 할까?
LC 또는 RC에서 뽑아오는데 여기서는 LC라고 가정하겠습니다
LC에서 LV를 뽑아서 k값으로 대체하고 T= LC로 변경한 다음에 다시 2번으로 올라가서 반복합니다.
5-way B-tree로 예제를 통해서 살펴보도록 하겠습니다
아래그림과 같은 트리가 있습니다.

여기서 만약 97을 지우고 싶다면 어떻게 해야 할까요?
1. 삭제할 k가 포함된 node T를 탐색합니다. (node T는 95, 97, 99 가 될 것입니다)
2. node T가 leaf node 인지 아닌지 확인합니다. ( 여기서 node T는 leaf node입니다)
3. leaf node라면 k를 삭제하고 MIN_KEY 조건을 위배하는지 검사합니다 (node T는 95, 99)
4. 5-way B-tree에서 MIN_KEY 조건은 최소 2개 이상의 값을 가져야 하므로, Node T는 2개 값을 가지므로 MIN_KEY 조건을 위배하지 않으니 종료합니다.
아래 그림은 97이 삭제된 후 트리입니다.

그러면 위의 트리에서 20을 삭제하면 어떻게 될까요?
1. 삭제할 k가 포함된 node T를 탐색합니다. (node T는 15, 20 이 될 겁니다)
2. node T가 leaf node 인지 아닌지 확인합니다. ( 여기서 node T는 leaf node입니다)
3. leaf node라면 k를 삭제하고 MIN_KEY 조건을 위배하는지 검사합니다 ( node T는 15)
4. 5-way B-tree에서 MIN_KEY 조건은 최소 2개 이상의 값을 가져야 하고, Node T는 1개의 값을 가지므로 MIN_KEY 조건을 위배합니다
5. MIN_KEY 조건을 위배했으므로 LS( 0, 5, 7) 또는 RS(30, 35, 37)에서 값을 가져올 수 있다면 가져와야 합니다.
6. LS(0, 5, 7)에서는 값을 가져와도 MIN_KEY조건을 위배하지 않으니까 값을 가져옵니다. 7이 부모로 올라가고 10이 node T로 내려가게 됩니다
아래 그림은 20이 삭제된 후 트리입니다.

그러면 위의 트리에서 10을 삭제하면 어떻게 될까요?
1. 삭제할 k가 포함된 node T를 탐색합니다. (node T는 10, 15 가 될 겁니다)
2. node T가 leaf node 인지 아닌지 확인합니다. ( 여기서 node T는 leaf node입니다)
3. leaf node라면 k를 삭제하고 MIN_KEY 조건을 위배하는지 검사합니다 ( node T는 15)
4. 5-way B-tree에서 MIN_KEY 조건은 최소 2개 이상의 값을 가져야 하고, Node T는 1개의 값을 가지므로 MIN_KEY 조건을 위배합니다
5. MIN_KEY 조건을 위배했으므로 LS( 0, 5) 또는 RS(30, 35, 37)에서 값을 가져올 수 있다면 가져와야 합니다.
6. LS(0, 5)에서는 값을 가져오면 MIN_KEY조건을 위배하니까 값을 가져오지 못하고 RS(30, 35, 37)에서는 값을 가져와도 MIN_KEY조건을 위배하지 않아서 값을 가져옵니다. node T로 25가 내려가게 되고 30이 부모로 올라가게 됩니다.
아래 그림은 10이 삭제된 후 트리입니다.

그러면 위의 트리에서 25를 삭제하면 어떻게 될까요?
1. 삭제할 k가 포함된 node T를 탐색합니다. (node T는 15, 25 가 됩니다)
2. node T가 leaf node 인지 아닌지 확인합니다. ( 여기서 node T는 leaf node입니다)
3. leaf node라면 k를 삭제하고 MIN_KEY 조건을 위배하는지 검사합니다 ( node T는 15)
4. 5-way B-tree에서 MIN_KEY 조건은 최소 2개 이상의 값을 가져야 하고, Node T는 1개의 값을 가지므로 MIN_KEY 조건을 위배합니다
5. MIN_KEY 조건을 위배했으므로 LS(0, 5) 또는 RS(35, 37)에서 값을 가져올 수 있다면 가져와야 합니다.
6. LS, RS 모두 값을 가져올 수 없는 상황입니다 (만약 가져오게 되면 LS 또는 RS가 MIN_KEY 조건을 위배하게 됩니다.)
7. 왼쪽으로 합치거나 오른쪽으로 합쳐야 합니다 왼쪽으로 합치게 되면 아래와 같은 그림의 모습이 됩니다

8. P에서 값을 하나 가져오면서 합치기 때문에 P가 MIN_KEY 조건을 어길 수 있는 상황이 생겼습니다. 실제로 P는 현재 값이 1개로 MIN_KEY 조건을 위배하고 있습니다. (5-way B-tree에서는 MIN_KEY 조건이 2개입니다)
9. P를 T로 놓고 다시 4번으로 올라갑니다 node T는 30으로 MIN_KEY 조건을 위배했으므로 LS 또는 RS에서 값을 가져올 수 있다면 가져야 와야 합니다. 이때 LS는 없고 RS는 75, 90, 105로 3개의 값을 가지고 있어 값을 가져와도 MIN_KEY 조건을 위배하지 않습니다. node T로 부모에서 40이 내려오게 오게 되고 RS에서 75가 부모로 올라가게 됩니다.
여기서는 node (65,70) 이 어디로 갈지 고민해 보시길 바랍니다
아래 그림은 25가 삭제된 후 트리입니다.

그러면 위의 트리에서 65를 삭제하면 어떻게 될까요?
1. 삭제할 k가 포함된 node T를 탐색합니다. (node T는 65, 70 이 됩니다)
2. node T가 leaf node 인지 아닌지 확인합니다. ( 여기서 node T는 leaf node입니다)
3. leaf node라면 k를 삭제하고 MIN_KEY 조건을 위배하는지 검사합니다 ( node T는 70)
4. 5-way B-tree에서 MIN_KEY 조건은 최소 2개 이상의 값을 가져야 하고, Node T는 1개의 값을 가지므로 MIN_KEY 조건을 위배합니다
5. MIN_KEY 조건을 위배했으므로 LS 또는 RS 에서 값을 빌려올 수 있으면 빌려와야 한다. 하지만 RS는 존재하지 않고 LS 또한 값을 빌려오게 되면 MIN_KEY 조건을 위배하기 때문에 빌려올 수 없다. 그렇기 때문에 왼쪽 또는 오른쪽으로 합치는 작업을 수행해야 한다.
6. 부모 노드의 오른쪽값으로는 합칠 수 없고 왼쪽 값으로만 합칠 수 있기 때문에 왼쪽으로 합치는 과정을 수행한다.
그렇게 되면 35, 37, 40, 65 가 30의 오른쪽 자식으로 구성되게 된다.
다음 그림은 합치는 과정을 수행한 후 모습입니다

7. P의 값 하나가 없어졌기 때문에 P를 다시 T로 하고 MIN_KEY 조건을 위배하는지 검사하게 된다. 값이 1개로 MIN_KEY 조건을 위배하게 됐으며 LS 또는 RS에서 값을 빌려올 수 있으면 빌려와야 합니다. 하지만 LS는 없고 RS 또한 값이 2개이기 때문에 한 개를 빌려오면 RS도 MIN_KEY 조건을 위배하기 때문에 빌려올 수 없습니다.
8. 어디에서도 빌려올 수 없기 때문에 T(30)와 root node P(75) 와 RS(90, 105)를 합칩니다.
다음 그림은 65가 삭제된 후 트리입니다.

이 정도면 node T가 leaf node 일 때 일어날 수 있는 상황들에 대해 거의 다룬 것 같습니다.
이제부터는 node T가 internal node일 때 일어나는 상황들에 대해서 알아보고자 합니다.
다음 그림에서 30을 삭제해 보도록 하겠습니다

1. 삭제할 k가 포함된 node T를 탐색합니다. (node T는 30, 40이 됩니다)
2. node T가 leaf node 인지 아닌지 확인합니다. ( 여기서 node T는 internal node입니다)
3. 여기서는 위에 지정했던 변수들을 사용할 것입니다. LC(left children) 에서 가장 큰 수를 LV 라고 하겠습니다. RC(right children) 에서 가장 작은 수를 RV 라고 하겠습니다. 여기서는 LV는 15 RV는 35가 될 것 입니다. LC는 값을 4개 가지고 있기 때문에 15를 부모로 올리더라도 MIN_KEY 제약을 위배하지 않습니다.(5-way B-tree 에서는 MIN_KEY 제약이 2개입니다)
아래 그림은 30이 삭제된 후 트리입니다.

그러면 여기서 105를 삭제하려면 어떻게 해야 할까요?
1. 삭제할 k가 포함된 node T를 탐색합니다. (node T는 90, 105)
2. node T가 leaf node인지 아닌지 확인합니다. (여기서 node T는 internal node)
3. LC(95, 99) 에서는 값을 가져올 수 없고 RC(110, 115, 120, 125) 에서는 값을 가져올 수 있습니다. RC에서 값을 가져와서 기존 k값(105)에 채워줍니다.
아래 그림은 105가 삭제된 후 트리입니다. ( 그림상 LC가 80, 85로 나오는데 95, 99가 되어야 맞는것 같습니다)

그러면 여기서 90을 삭제하려면 어떻게 해야 할까요?
1. 삭제할 k가 포함된 node T를 탐색합니다. (node T는 90, 110)
2. node T가 leaf node인지 아닌지 확인합니다. (여기서 node T는 internal node)
3. LC와RC에서 값을 가져올 수 없습니다. (MIN_KEY 조건을 위배하기 때문에)
4. 그렇게 되면 LC 또는 RC에서 값을 가져와서 k값으로 대체 하는데 저희는 LC에서 LV값(85)을 가져온다고 하겠습니다.
그러면 LC는 80값이 하나 남을 것이고 T 를 LC로 놓고 위로 올라가게 됩니다.

5. RS에서 값을 빌려오게 되면 RS가 MIN_KEY 조건을 위배하기 때문에 빌려올 수 없습니다. 그렇기 때문에 T, PLV, RS를 merge 합니다.
6. P에서 85를 뽑아서 왼쪽자식으로 내렸기 때문에 P는 110 혼자 남게 되고 이는 즉 MIN_KEY 조건을 위배하게 됩니다.

7. 왼쪽에서 값을 빌려올 수 없기 때문에 T와 PLV, LS를 합치게 됩니다
아래 그림은 90이 삭제된 후 트리입니다.

'CS > 데이터베이스' 카테고리의 다른 글
동시성 제어(Concurrency Control) (0) 2021.12.12 동시 트랜잭션(Concurrent Transaction) (0) 2021.12.09 트랜잭션(Transaction)이란? (0) 2021.11.23 B+Tree 검색, 삽입, 삭제 (0) 2021.11.17 B-Tree 와 B+Tree (0) 2021.11.12