B-Tree 와 B+Tree

B-Tree란?

데이터베이스와 파일 시스템에서 널리 사용되는 트리 자료구조의 일종으로 , 이진트리를 확장해 하나의 노드가 가질 수 있는 자식 노드의 최대 숫자가 2보다 큰 트리 구조입니다.

 

많은 자료구조중에 하필 왜 B-Tree를 사용하는 것일까?

탐색 시간이 제일 빠른 해시 테이블을 DB 인덱스로 사용할 수 없는 이유

모든 자료구조와 어떤 알고리즘을 비교해도 탐색 시간이 가장 빠른 것은 바로 해시 테이블이다. 해시 테이블은 해시 함수를 통해 나온 해시 값을 이용하여 저장된 메모리 공간에 접근하기 때문에 O(1)이라는 시간 복잡도를 가진다.

하지만 '단 하나의 데이터를 탐색하는 시간'에만 O(1)이며 우리는 DB에서 (=) 뿐만 아니라 (<, >) 부등호를 사용하기 때문에 해시 테이블은 DB 인덱스에 어울리지 않는다.

 

또 다른 Blanced Tree인 RedBlack-Tree가 DB 인덱스로 선택 받지 못한 이유

B-Tree는 노드 하나에 여러 데이터가 저장될 수 있지만 RedBlack-Tree는 노드에 하나의 데이터를 저장한다. 따라서 RedBlack-Tree는 참조 포인터로 메모리에 접근해야 하고, B-Tree의 경우에는 배열로 접근이 가능해서 탐색 시간이 B-Tree가 더 빠를 수밖에 없다.

 

그러면 배열을 쓰면 되는거 아닌가?

탐색 속도로만 본다면 B-Tree보다 훨씬 빠르고, 데이터들이 정렬 상태를 유지할 수 있으므로 부등호(<,>) 연산에도 문제가 없다. 하지만 탐색만 빠를 뿐 데이터 저장, 삭제가 일어나는 순간 B-Tree 보다 훨씬 비효율적인 성능이 발생하기 때문에 사용하지 않는다.

 

 

트리구조는 최악의 경우 아래 그림과 같은 선형자료구조와 같은 구조를 가질 수 있습니다.

B-Tree는 이러한 구조를 막기 위해 나오게 되었는데 삽입, 삭제 부분 속도를 희생하는 대신 탐색의 속도를 일정하게 향상해 안정적 데이터 검색이 이루어질 수 있도록 고려한 인덱스 구조입니다.

 

항상 단말노드들이 동일한 높이를 가지기 때문에 균형 잡힌 트리 Blacned-Tree라고 불립니다.

 

한 노드에 M개의 자료가 배치되면 M차 B-Tree 또는 M-way B-Tree 라고 한다.

 

다음 그림은 5차 B-Tree, 5-way tree의 예시입니다.

B-Tree의 특징

1. 노드의 자료수가 K라면, 자식의 수는 K+1 개이어야 한다.

 

2. 자료는 정렬된 상태로 저장된다.

 

3. 한 노드 N의 왼쪽 서브 트리는 N보다 작은 값으로 되어 있고, 오른쪽 서브 트리는 N보다 큰 값으로 되어 있다.

 

4. 루트 노드는 적어도 2개 이상의 자식을 가져야 한다.(트리가 ROOT 노드로만 구성되어 있을 경우는 제외)

 

5. 루트 노드를 제외한 모든 노드는 적어도 [M/2] 개의 키를 가지고 있어야 한다.

 

6. 리프 노드로 가는 경로의 길이는 모두 같다

 

7. 입력 자료는 중복될 수 없다.

 

위의 특징이 잘 이해되지 않는다면 다음 링크에서 직접 M-way B-Tree에 데이터를 넣어보면 시각화가 구현되어 있어 이해하기 좋습니다.

https://www.cs.usfca.edu/~galles/visualization/BTree.html

B-Tree Visualization

B+Tree 란?

B-Tree의 변형된 형태로 인덱스구조에서 순차 접근에 대한 문제의 해결책으로 제시되었습니다.

B-Tree는 노드의 값이 Unique 하지만 B+Tree 에서는 right 노드와 right의 부모 노드에서 공존할 수 있고, 기존 B-Tree + 데이터의 연결 리스트 구조로 이루어져 있어 순차적인 탐색에 매우 유리합니다.

 

B+Tree는 아래와 같은 그림의 구조를 가집니다.

 

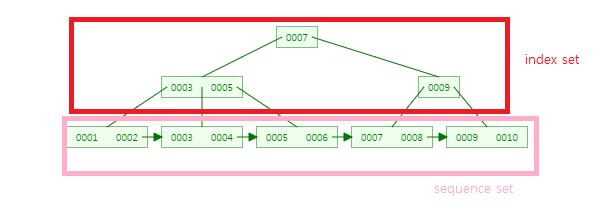
다음링크는 B+Tree의 시각화가 구현되어 있는 링크입니다.

https://www.cs.usfca.edu/~galles/visualization/BPlusTree.html

B+ Tree Visualization

 

 

 

 

출처

https://helloinyong.tistory.com/296

데이터베이스 인덱스는 왜 'B-Tree'를 선택하였는가

https://matice.tistory.com/8

[OS] 책 설명이 x같아서 내가 쉽게 쓴 B 트리