-
3124. 최소 스패닝 트리 - 자바(JAVA)알고리즘/SW Expert Academy 2022. 5. 16. 00:01반응형
https://swexpertacademy.com/main/code/problem/problemDetail.do?contestProbId=AV_mSnmKUckDFAWb
SW Expert Academy
SW 프로그래밍 역량 강화에 도움이 되는 다양한 학습 컨텐츠를 확인하세요!
swexpertacademy.com
문제 해석
그래프가 주어졌을 때, 그 그래프의 최소 스패닝 트리를 구하는 프로그램을 작성하세요.
최소 스패닝 트리는, 주어진 그래프의 모든 정점들을 연결하는 부분 그래프 중에서 그 가중치의 합이 최소인 트리를 말합니다.
입력으로 주어지는 그래프는 하나의 연결 그래프임이 보장됩니다.
문제 풀이 전 설계
스패닝 트리를 계산하는 알고리즘으로는 프림 알고리즘과 크루스 칼 알고리즘이 존재합니다.
본 문제에서는 주어지는 정점과 간선의 개수가 많습니다.
따라서 프림 알고리즘을 이용할 경우에는 힙을 사용하고 크루스칼 알고리즘을 이용할 경우에는 유니온 파인드 알고리즘을 사용해야 합니다.
프림 알고리즘은 임의의 정점을 선택하고 최소간선을 선택하면서 정점을 추가해나가는 알고리즘입니다.
다음 해설을 듣고 정리한 내용입니다.
https://www.youtube.com/watch?v=Qgqubl1nW7I
1. 임의의 정점 A를 선택했습니다.

2. A에서 갈 수 있는 최소인 9를 선택하여 A -> F로 이동합니다.

3. 현재 집합은 {A, F}입니다.
F에서 갈 수 있는 E는 25의 비용을 가집니다.
A에서 B로 갈 수 있는 비용은 27의 비용을 가집니다.
따라서 E를 선택하고 이동합니다.
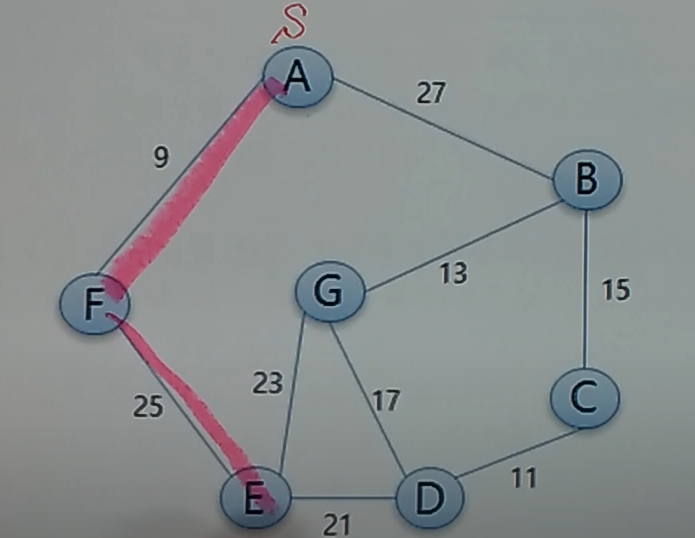
4. 이런 방식으로 최소를 탐색하게 되면 마지막 결과는 다음과 같습니다.

문제 풀면서
양방향 트리인점을 간과하여 단방향 트리로 설계하였으며 방문 체크를 유의해서 했어야 했습니다.
코드
import java.io.BufferedReader; import java.io.IOException; import java.io.InputStreamReader; import java.util.*; public class Solution_3124_최소스패닝트리 { static class EdgeInfo{ int to; long cost; public EdgeInfo(int to, long cost) { this.to = to; this.cost = cost; } } public static void main(String[] args) throws IOException { BufferedReader br = new BufferedReader(new InputStreamReader(System.in)); int t = Integer.parseInt(br.readLine()); List<ArrayList<EdgeInfo>> edges= null; StringBuilder sb = new StringBuilder(); for(int tc=1; tc<=t; tc++) { long result = 0; edges= new ArrayList<>(); StringTokenizer st = new StringTokenizer(br.readLine()," "); int Vertex = Integer.parseInt(st.nextToken()); int Edge = Integer.parseInt(st.nextToken()); for (int i = 0; i <= Vertex; i++) { edges.add(new ArrayList<EdgeInfo>()); } for (int i = 0; i < Edge; i++) { st = new StringTokenizer(br.readLine(), " "); int from = Integer.parseInt(st.nextToken()); int to = Integer.parseInt(st.nextToken()); long cost = Integer.parseInt(st.nextToken()); edges.get(from).add(new EdgeInfo(to, cost)); edges.get(to).add(new EdgeInfo(from,cost)); } PriorityQueue<EdgeInfo> edgeSet = new PriorityQueue<EdgeInfo>((e1,e2) -> (int) (e1.cost - e2.cost)); boolean[] visited = new boolean[Vertex+1]; //임의의 정점부터 시작하므로 1번 정점부터 시작 = 트리는 항상 연결되어있음 for(EdgeInfo e : edges.get(1)){ edgeSet.add(e); } visited[1] = true; int count = 1; boolean isAllVisited = false; while(!edgeSet.isEmpty()){ if(count == Vertex){ break; } //정점과 연결된 간선중이 최솟값으로 이동 EdgeInfo curEdge = edgeSet.poll(); if(visited[curEdge.to]){ continue; } //방문체크해줌 visited[curEdge.to] = true; count++; //이동한 간선에 대해 이동 for(EdgeInfo e : edges.get(curEdge.to)){ //이미 방문된 노드로는 전파하지 않음 if(visited[e.to]){ continue; } //그렇지 않으면 후보리스트에 추가 edgeSet.add(e); } result += curEdge.cost; } sb.append("#" + tc + " " + result + "\n"); } System.out.print(sb.toString()); } }'알고리즘 > SW Expert Academy' 카테고리의 다른 글
3307. 최장 증가 부분 수열 (0) 2022.05.20 1263. [S/W 문제해결 응용] 8일차 - 사람 네트워크2 (0) 2022.05.20 1218. [S/W 문제해결 기본] 4일차 - 괄호 짝짓기 (0) 2022.05.01 5432. 쇠막대기 자르기 - 자바(JAVA) (0) 2022.04.15 7465. 창용 마을 무리의 개수 - 자바(JAVA) (0) 2022.04.09
