-
[백준] 10830번 : 행렬 제곱 - 자바(JAVA)알고리즘/백준 2022. 3. 6. 00:01반응형
https://www.acmicpc.net/problem/10830
10830번: 행렬 제곱
크기가 N*N인 행렬 A가 주어진다. 이때, A의 B제곱을 구하는 프로그램을 작성하시오. 수가 매우 커질 수 있으니, A^B의 각 원소를 1,000으로 나눈 나머지를 출력한다.
www.acmicpc.net
문제 해석
크기가 N*N인 행렬 A가 주어진다.
이때 A의 B제곱을 구하는 프로그램을 작성하라.
수가 매우 커질 수 있으므로 A^B의 각 원소를 1,000으로 나눈 나머지를 출력한다.
입력
첫째 줄에 행렬의 크기 N과 B가 주어진다.
둘째 줄부터 N개의 줄에 행렬의 각 원소가 주어진다.
제약조건
2 ≤ N ≤ 5
1 ≤ B ≤ 100,000,000,000
행렬의 각 원소는 1,000보다 작거나 같은 자연수 또는 0이다.
출력
첫째 줄부터 N개의 줄에 걸쳐 행렬 A를 제곱한 결과를 출력한다.
문제 풀이 전 설계
B의 경우에는 입력을 받을 때 int형의 범위를 넘어가기 때문에 long 타입을 사용해야 한다.
행렬의 연산을 해야 하기 때문에 행렬의 연산하는 법을 알아야 한다.
행렬의 연산 법
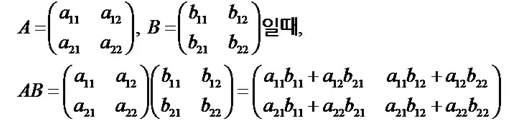
이를 일반화시킨다면
AB(i, j) = A의 i번째 row의 요소 x B의 j번째 column의 요소의 합입니다.
이것을 프로그래밍화 시킨다면
AB [i][j] = A [0][i] * B [j][0] + A [1][i] * B [j][1] +..... + A [N-1][i] * B [j][N-1]입니다.
행렬의 연산은 다음과 같이 진행하면 될 것 같습니다.
static int[][] multiplyMartix(int[][] a, int[][] b) { int result[][] = new int[N][N]; for (int i = 0; i < N; i++) { for (int j = 0; j < N; j++) { for (int k = 0; k < N; k++) { result[i][j] += (a[i][k] * b[k][j]); result[i][j] %= 1000; } } } return result; }해결해야 하는 과제 중 하나는 B의 범위가 천억입니다.
따라서 어떤 행렬 A에 대하여 A^B를 해야 하므로 최악의 경우 A^천억 번 발생할 수 있습니다.
또한 행렬의 수의 범위는 0~1000 사이의 자연수입니다.
만약 A의 모든 원소가 1,000이라면....
A^2 = 하나의 원소가 1000*1000 + 1000*1000 = 2,000,000
A^4 = 하나의 원소가 2,000,000* 2,000,000 + 2,000,000* 2,000,000 = 8,000,000,000,000
으로 기하급수적으로 늘어납니다.
가장 큰 타입인 Long에 담을 수 있는 값은 아래와 같습니다.
Long.MAX_VALUE = 9223372036854775807따라서 문제의 조건을 사용해야 합니다.
수가 매우 커질 수 있으므로 A^B의 각 원소를 1,000으로 나눈 나머지를 출력한다.
우리가 집중해야 할 부분은 1,000으로 나눈 나머지이므로 백의 자리인 세 자리 숫자만 신경 쓰면 됩니다.
이를 알아보기 위해 곱셈을 조금 살펴보겠습니다.
4 x 4 = 16
4 x 14 = 56
4 x 24 = 96
4 x 34 = 136
11 x 11 = 121
21 x 11 = 231
어떤 특성을 찾으셨나요?
곱셈하는 두 수의 일의 자리 숫자가 같다면 일의 자리의 곱셈 결과는 항상 동일합니다. (위에서는 6과 1이 동일)
더 살펴보겠습니다.
21 x 11 = 231
121 x 11 = 1,331
121 x 211 = 25,531
곱셈하는 두 수의 십의 자리 숫자가 같다면 십의 자리까리 곱셈 결과는 항상 동일합니다. ( 위에서는 31이 동일)
41 x 37 = 1,517
141 x 37 = 5,217
141 x 537 = 75,717
곱셉 하는 두 수의 십의 자리 숫자가 같다면 십의 자리까지 곱셈 결과는 항상 동일합니다. ( 위에서는 17로 동일)
다음은 백의 자리의 곱셈 결과도 동일한지 보겠습니다
157 x 634 = 99,538
5,157 x 3,634 = 18,740,538
1,157 x 634 = 733,538
곱셈하는 두 수의 백의 자리 숫자가 같다면 백의 자리까지 곱셈 결과는 항상 동일합니다.
우리가 집중해야 할 부분은 1,000으로 나눈 나머지이므로 백의 자리인 세 자리 숫자만 신경 쓰면 됩니다.
따라서 연산의 결과가 얼마나 큰 수가 나오는지는 상관없습니다.
백의 자리만 계속 추적하면 됩니다.
따라서 157 x 634 = 99,538이 나온다면? 우리는 538만 사용하면 됩니다.
이렇게 연산의 결과를 확 줄여버릴 수 있습니다.
이제 실제로 문제를 풀어보겠습니다.
문제를 풀던 도중 B의 범위가 1~ 천억 인 것이 생각나서 O(N)의 시간 복잡도로 풀다가 아 이건 O(N)으로 풀면 1000초가 걸리겠구나 생각이 들었습니다.(보통 cpu 연산 1억 번 = 1초)
따라서 O(log(N)) 까지 시간 복잡도를 줄여야겠다는 생각이 들었습니다.
이진 탐색이 가장 먼저 떠올랐습니다.
예를 들어 행렬 M에 대한 M^14를 진행해보겠습니다.

위의 그림과 같이 M^14 = M^7 * M^7으로 나타낼 수 있습니다. (14는 짝수)
M^7 = M^3 * M^3 * M^1 (7은 홀수)
M^3 = M^1 * M^1 * M^1 (3은 홀수)
재귀 함수를 호출하여 스택에 모두 쌓이게 되면 연산이 시작됩니다.
M^1을통해 M^2를 만들고 M^1을 곱하여 M^3 이 만들어지게 됩니다.
그러면 M^3을 통해 M^6을 만들고 M^1을 곱하여 M^7이 만들어집니다.
그러면 M^7을 통해 M^14를 만들고 연산이 종료됩니다.
따라서 연산의 시간복잡도가 Log(N)인 알고리즘이 완성됩니다.
코드
package day0208; import java.io.BufferedReader; import java.io.IOException; import java.io.InputStreamReader; import java.util.StringTokenizer; public class Main_10830_행렬제곱 { final static int MOD = 1000; static long repeatCount; static int matrix[][]; static int result[][]; static int origin[][]; static int N; public static void main(String[] args) throws IOException { inputMartixInfo(); calculateMartix(repeatCount); printResult(); } private static void inputMartixInfo() throws IOException { BufferedReader br = new BufferedReader(new InputStreamReader(System.in)); StringTokenizer st = new StringTokenizer(br.readLine(), " "); N = Integer.parseInt(st.nextToken()); repeatCount = Long.parseLong(st.nextToken()); matrix = new int[N][N]; result = new int[N][N]; for (int i = 0; i < N; i++) { st = new StringTokenizer(br.readLine(), " "); for (int j = 0; j < N; j++) { matrix[i][j] = Integer.parseInt(st.nextToken()); } result[i][i] = 1; } } private static void calculateMartix(long cnt) { // 필요한 시간복잡도 = O(log(N)) /* * while (repeatCount > 0) { if (repeatCount % 2 == 1) { result = * multiplyMartix(result, matrix); } matrix = multiplyMartix(matrix, matrix); * repeatCount /= 2; } */ if (cnt == 1) { result = multiplyMartix(result, matrix); return; } calculateMartix(cnt / 2); // 짝수 if (cnt % 2 == 0) { result = multiplyMartix(result, result); return; } // 홀수 int[][] temp = multiplyMartix(result, matrix); result = multiplyMartix(result, temp); return; } // 두 행렬a와 b에 대한 곱 연산 : a x b static int[][] multiplyMartix(int[][] a, int[][] b) { int result[][] = new int[N][N]; for (int i = 0; i < N; i++) { for (int j = 0; j < N; j++) { for (int k = 0; k < N; k++) { result[i][j] += (a[i][k] * b[k][j]); result[i][j] %= MOD; } } } return result; } static void printResult() { StringBuilder sb = new StringBuilder(); for (int i = 0; i < N; i++) { for (int j = 0; j < N; j++) { sb.append(result[i][j]).append(' '); } sb.append('\n'); } System.out.print(sb); } }'알고리즘 > 백준' 카테고리의 다른 글
[백준] 1275번 : 커피숍2 - 자바(JAVA) (0) 2022.03.13 [백준] 7562 : 나이트의 이동 - 자바(JAVA) (0) 2022.03.09 [백준] 2493 : 탑 - 자바(JAVA) (0) 2022.03.05 [백준] 11047번 : 동전 0 - 자바(JAVA) (0) 2022.02.28 [백준] 7576번 : 토마토 (0) 2022.02.25