[프로그래머스] 2021 카카오 채용연계형 인턴십 - 미로 탈출 - 자바(JAVA)
https://programmers.co.kr/learn/courses/30/lessons/81304
코딩테스트 연습 - 미로 탈출
4 1 4 [[1, 2, 1], [3, 2, 1], [2, 4, 1]] [2, 3] 4
programmers.co.kr
문제 해석
1번부터 3번까지 번호가 붙어있는 3개의 방이 있고, 방과 방 사이를 연결하는 길에는 이동하는 걸리는 시간이 표시되어있습니다.
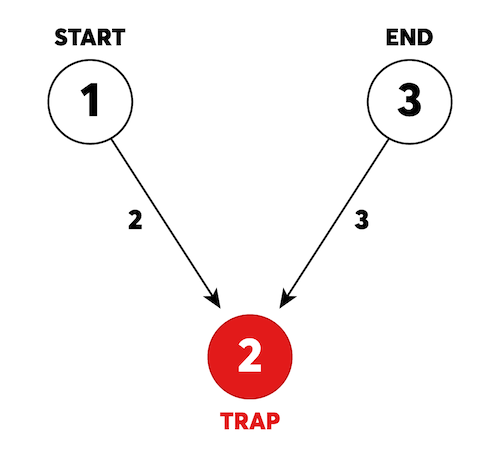
화살표가 가리키는 방향으로만 이동할 수 있습니다. (단방향 그래프)
미로에는 함정이 존재하며 함정으로 이동하면 이동한 함정과 연결된 모든 화살표의 방향이 바뀝니다.
출발지점인 start에서 end로 이동하는데 걸리는 최소 시간을 구하려고 합니다.
문제 풀이 전 설계
서로 다른 두 방 사이에 직접 연결된 길이 여러 개 존재할 수도 있습니다. (더 작은 값으로만 갱신)
그래프의 최단거리를 구하는 문제이므로 다익스트라가 생각나는 문제인데 TRAP이라는 함정이 존재하는걸 잘 고려해야 할 것 같습니다.

다익스트라 기준으로 탐색하며 해당 노드를 한번만 방문하는 것이 아니라 여러 번 방문할 수 있을 거 같습니다.
하지만 2번을 초과해서 방문하는 경우는 필요없어 보입니다. (2->3을 반복하면 비용이 증가함)
(2번인 이유는 위의 그림처럼 1->2를 방문하는 순간 2->4로 갈 수 없어지고 3을 한번 들려야지 다시 방향에 도달할 수 있기 때문에)
문제 풀이하면서
다익스트라와 비트마스킹을 활용한 문제였습니다.
신기한 점은 비트 마스킹을 활용하여 해당 트렙이 발동되었는지를 10개의 비트로 체크하고(트랩이 최대 10개이기 때문)
트렙이 발동된것을 확인함으로써 graph [from][to]로 이동해야 했던 것을 graph [to][from]을 활용하여 해결하였습니다.
2번만 방문하면 될것같다는 생각까지만 가고 이것을 비트 마스킹을 활용한 방문 체크 + 트랩 체크까지 생각을 확장하지 못했던 것 같습니다.
코드
import java.util.*;
class Solution {
//최대크기가 1000이고 index로 쓰기위해 1001
private final static int MAX_N = 1001;
private final static int INF = Integer.MAX_VALUE;
static int[][] graph = new int[MAX_N][MAX_N];
int dijkstra(int n, int src, int dst, int[] traps){
//첫번째 인자가 가중치
PriorityQueue<int[]> pq = new PriorityQueue<>((c1,c2) -> c1[0] - c2[0]);
//Trap이 10개이기때문에 10개bit 사용
boolean[][] visited = new boolean[MAX_N][1 << 10];
pq.add(new int[]{0, src, 0});
while(!pq.isEmpty()){
int[] curr = pq.poll();
int weight = curr[0];
int index = curr[1];
int state = curr[2];
//목적지 도착
if(index == dst) return weight;
//방문체크
if(visited[index][state]) continue;
visited[index][state] = true;
boolean currTrapped = false;
HashMap<Integer, Boolean> trapped = new HashMap<>();
for(int i=0; i< traps.length; i++){
int bit = 1 << i;
//현재 함정체크가 되어있음
if((state & bit) != 0){
//현재 함정체크가 되어잇는데 또 방문했음
if(traps[i] == index){
//비트를 꺼줘야 함
state &= ~bit;
} else{
trapped.put(traps[i],true);
}
} else {
//현재 함정체크가 되어있지 않음
if(traps[i] == index){
//함정체크를 위한 해당 비트를 켜줌
state |= bit;
trapped.put(traps[i], true);
currTrapped = true;
}
}
}
for(int v=1; v<=n; v++){
if(v == index) continue;
boolean nextTrapped = trapped.containsKey(v) ? true : false;
if(currTrapped == nextTrapped){
if(graph[index][v] != INF){
pq.add(new int[]{weight + graph[index][v], v, state});
}
} else{
if(graph[v][index] != INF)
pq.add(new int[]{weight + graph[v][index], v , state});
}
}
}
return INF;
}
public int solution(int n, int start, int end, int[][] roads, int[] traps) {
//그래프 INF로 초기화
for(int i= 1; i <= n; i++){
for(int j=1; j<=n; j++){
if(i==j) graph[i][j] = 0;
else graph[i][j] = INF;
}
}
//그래프 설정
for(int[] data : roads){
int from = data[0], to = data[1], weight = data[2];
if(weight < graph[from][to])
graph[from][to] = weight;
}
int answer = dijkstra(n, start, end, traps);
return answer;
}
}
출처
https://www.youtube.com/watch?v=B1CjIauForM