가장 빠르게 소수를 찾는 방법

소수란?

자신보다 작은 두 개의 자연수를 곱하여 만들 수 없는, 1보다 큰 자연수입니다.

https://jm-park.github.io/algorithm/2018/08/06/Prime-Number(%EC%86%8C%EC%88%98)-%ED%8C%90%EB%B3%84%EB%B2%95-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98.html

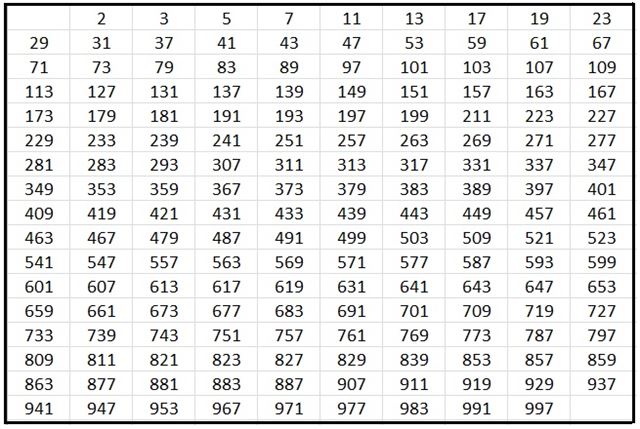
방법 1: 가장 간단한 방법

N이 소수인지 판별하기 위해서는 2 ~ N-1까지 나누어서 하나라도 나누어 떨어지는가를 확인하는 방법이 있습니다.

 

이는 한개의 숫자에 대해 소수인지 파별하기 위해서는 O(N)의 시간 복잡도를 가지며 N개의 수에 대해서는 O(N^2)의 시간 복잡도를 가집니다.

 

방법 2 : 제곱근

만약 12에 대하여 소수를 판별하려고 합니다.

12의 약수는 1, 2, 3, 4, 6, 12를 가집니다.

 

가장 간단한 방법처럼 12를 2부터 N-1까지 나누어보려고 할 때 2* 6 = 6 * 2의 성질을 이용한 방법입니다. (xy = yx)

제곱근을 기준으로 제좁근까지 나누어 떨어지는지 여부를 조사하면 더 빠르게 소수 판별이 가능합니다.

 

시간 복잡도 : O(sqrt(n))

 

방법 3: 에라토스테네스의 체 - 대량의 소수 얻기

 

방법 2처럼 n에 대한 약수로 접근하는 것이 아니라, n의 배수를 기반으로 접근합니다.

 

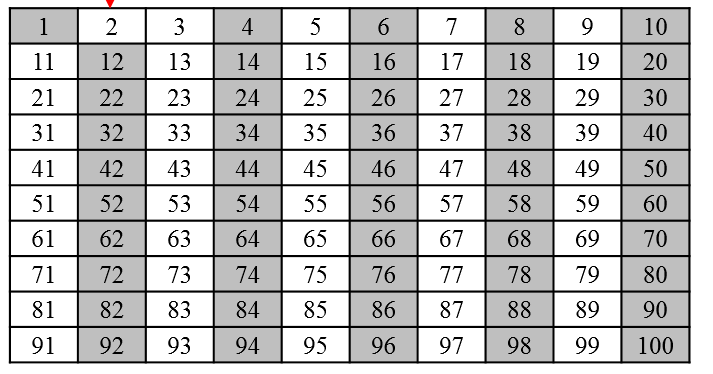
에라토스테네스의 체를 사용하여 1~100까지의 수가 소수인지 판별해 보겠습니다.

 

먼저 1은 소수가 아니므로 제외합니다.

https://library-of-k.tistory.com/79

2부터 시작해서 소수를 찾으면서 합성수를 제거해 나갑니다.

2의 배수들은 모두 2를 약수로 가지므로 2의 배수들을 제외합니다.

https://library-of-k.tistory.com/79

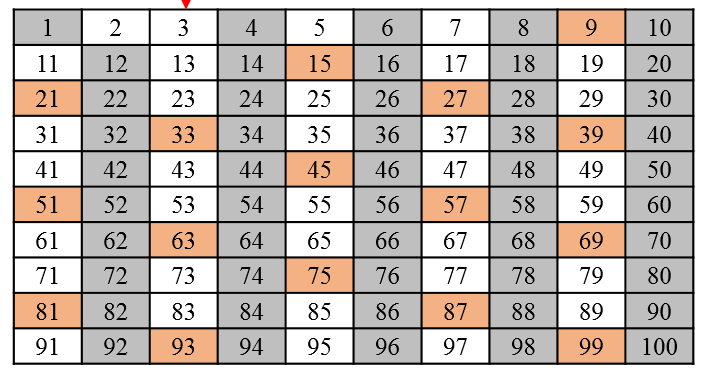
이제 다음으로 제외되지 않은 가장 작은 수 3을 선택하고, 3의 배수들을 제외합니다.

https://library-of-k.tistory.com/79

 

다음으로 제외되지 않은 가장 작은 수인 5를 선택하고, 5의 배수를 제외합니다.

https://library-of-k.tistory.com/79

다음으로 제외되지 않은 가장 작은 수인 7을 선택하고, 7의 배수를 제외합니다.

https://library-of-k.tistory.com/79

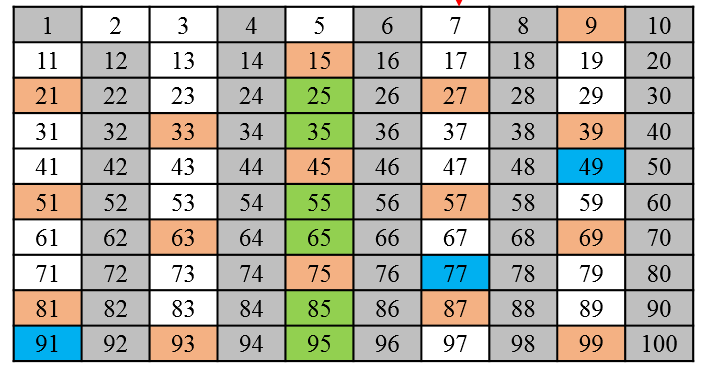
다음으로는 11, 13, 17 ~.... ~ 97 등의 수를 선택하여 배수를 제외하지만 배수가 존재하지 않습니다.

따라서 남아있는 하얀 수들이 소수가 됩니다.

 

시간복잡도 : O(NloglogN)

public class 에스토스테네스의체 {

	public static void main(String[] args) {
		// TODO Auto-generated method stub
		int targetNum = 100;
		boolean[] primeArray = new boolean[targetNum + 1];

		for (int i = 2; i < targetNum; i++) {
			if (primeArray[i]) {
				continue;
			}
			for (int j = i*i; j < targetNum; j+=i) {
				if (primeArray[j])
					continue;
				if (j % i == 0) {
					primeArray[j] = true;
				}
			}
		}
		
		for(int i=2; i<targetNum; i++) {
			if(primeArray[i]) {
				continue;
			}
			System.out.println(i);
		}
	}

}

 

 

출처

https://jm-park.github.io/algorithm/2018/08/06/Prime-Number(%EC%86%8C%EC%88%98)-%ED%8C%90%EB%B3%84%EB%B2%95-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98.html 

JM's IT Blog

https://library-of-k.tistory.com/79

효율적으로 소수 구하기 - 에라토스테네스의 체 (Sieve of Eratosthenes)

https://en.wikipedia.org/wiki/Sieve_of_Eratosthenes#Algorithm_complexity

Sieve of Eratosthenes - Wikipedia