[백준] 3176번 : 도로 네트워크 - 자바(JAVA)

https://www.acmicpc.net/problem/3176

3176번: 도로 네트워크

 

문제 해석

N개의 도시와 그 도시를 연결하는 N-1개의 도로로 이루어진 도로 네트워크가 존재합니다.

모든 도시의 쌍에는 그 도시를 연결하는 유일한 경로가 있고, 각 도로의 길이는 입력으로 주어집니다.

총 K개의 도시 쌍이 주어질 때, 경로 상에서 가장 짧은 도로의 길이와 가장 긴 도로의 길이를 구하는 프로그램을 작성하세요

 

문제 풀이 전 설계

N개의 도시와 N-1개의 도로 / 도시를 연결하는 유일한 경로가 존재합니다.

최소 신장 트리인 MST가 생각나는 문제입니다.

여기서는 최대인 경우도 구해야 하기 때문에 최소 신장 트리를 조금 응용해서 최대로 만들면 좋을 것 같습니다.

 

또한 도로의 길이가 백만, N의 범위가 10만이기 때문에 출력을 위한 변수는 int가 아닌 long으로 선언합니다.

 

하지만 실제로 문제의 그래프를 보고 예제 입력을 본다면 MST를 구현하는 문제는 아닌 것 같습니다.

예제1,2를 그려본 그래프

MST가 주어지고 거기서 D -> E로 이동할 때 가장 짧은 도로와 긴 도로를 찾아내는 것입니다.

 

임의의 D -> E가 주어지고 가장 짧은 도로와 긴 도로를 찾아내는 가장 간단하게 떠오르는 방법은 DFS로 D에서 출발해서 E에 도착할 때까지 최소/최대 비용을 갱신해나가면서 마지막에 출력하는 것입니다.

 

하지만 인접 리스트의 DFS의 시간 복잡도는 (N+e)입니다.

이것을 K번 반복한다면 결국에 O(10만 * 10만)의 시간 복잡도를 가지기 때문에 문제를 해결할 수 없습니다.

 

뭔가 세그먼트 트리를 사용한다면 어떨까?라는 생각이 듭니다.

하지만 문제는 각각의 임의의 정점에 어떤 포함관계를 가지고 있는지 확인할 수 없습니다.

 

LCA(Lowest Common Ancestor) 풀이 방식으로 두 노드의 부모 노드를 구한 다음 세 노드의 정보를 이용해서 최소, 최대 거리를 찾게 되면 O(NM)이라는 시간 복잡도를 가지게 되어 시간 초과가 발생할 수 있습니다.

 

좀 더 효율적인 방법으로 LCA + DP를 활용하여 2^h 부모 노드에 대한 데이터를 다루며 시간 복잡도를 O(MlogN)까지 줄일 수 있습니다.

 

조상 노드로 거슬로 올라가는 단위가 2^h번째 꼴이기 때문에 한 번의 Query 연산의 시간 복잡도를 logN으로 줄일 수 있습니다.

 

어떤 방식 인치 천천히 이해해보겠습니다.

 

각각의 노드의 깊이와 해당 노드에서 2^N 번째 부모의 값을 메모해 놓습니다.

모든 부모를 저장한다면 시간이 너무 오래 걸리고, 메모리 공간을 많이 차지하기 때문에 2^N번째 부모 노드 값만 저장합니다.

 

2^N번째라는 말이 잘 이해가 되지 않았는데 그냥 1번째, 2번째, 4번째... 8번째... 2^N번째 부모를 저장한다는 이야기입니다.

 

https://devowen.com/274

이런 식으로 4번과 12번 노드에 대해서 각각의 깊이와 2^N번째 조상을 메모했습니다.

그러고 나서 깊이가 더 깊은 노드를 깊이가 얕은 노드까지 올려주는 작업을 진행합니다.

 

12번 노드의 깊이가 더 깊기 때문에 깊이를 4번 노드와 맞춰줍니다.

 

이때는 항상 역순으로 탐색해줍니다. 2^1 조상인 3을 먼저 탐색하고 높이가 더 높기 때문에 그 아래인 2^0 조상인 7을 탐색합니다.

 

2^0번째 조상이 4번노드와 깊이가 같아지므로 그 지점까지 노드를 끌어올립니다.

 

 

https://devowen.com/274

이제 깊이가 같아졌습니다.

같은 높이씩 올리면서 공통 조상을 찾습니다.

이때도 2^N번째 조상부터 역순으로 탐색하며 2^N번째 조상이 같으면 패스하고, 달라질 때마다 노드를 타고 올라갑니다.

 

 

LCA에 대해서 어느 정도 알아보았으니 이제 문제로 들어가 보겠습니다.

 

1. 인접 리스트로 배열을 구성합니다.

        int from,to,distance;
        for (int i = 1; i <= N-1; i++) {
            st = new StringTokenizer(br.readLine());
            from = Integer.parseInt(st.nextToken());
            to = Integer.parseInt(st.nextToken());
            distance = Integer.parseInt(st.nextToken());
            // 양방향 간선
            tree[from].add(new edge(to, distance));
            tree[to].add(new edge(from, distance));
        }

 

2. root 노드를 1로 설정한 뒤 DFS로 트리를 만들어줍니다.

이때 각각의 노드를 연결하면서 첫 번째 부모와 부모의 최대/최소 도로 길이를 dp배열에 저장합니다.

    // DEPTH 확인 DFS
    static void dfs(int id, int cnt) {
        // 1. depth를 기록
        depth[id] = cnt;

        // 2. 자식들의 depth를 기록
        int len = tree[id].size();
        for (int i = 0; i < len; i++) {
            edge next = (edge) tree[id].get(i);
            if (depth[next.target] != 0) {
                continue;
            }
            // 아직 깊이를 모르면 → 미방문 노드
            dfs(next.target, cnt+1);
            parent[0][next.target] = id;		// 첫번째 부모를 기록

            minDist[0][next.target] = next.cost; // 현재 cost로 갱신
            maxDist[0][next.target] = next.cost; // 현재 cost로 갱신
        }
        return;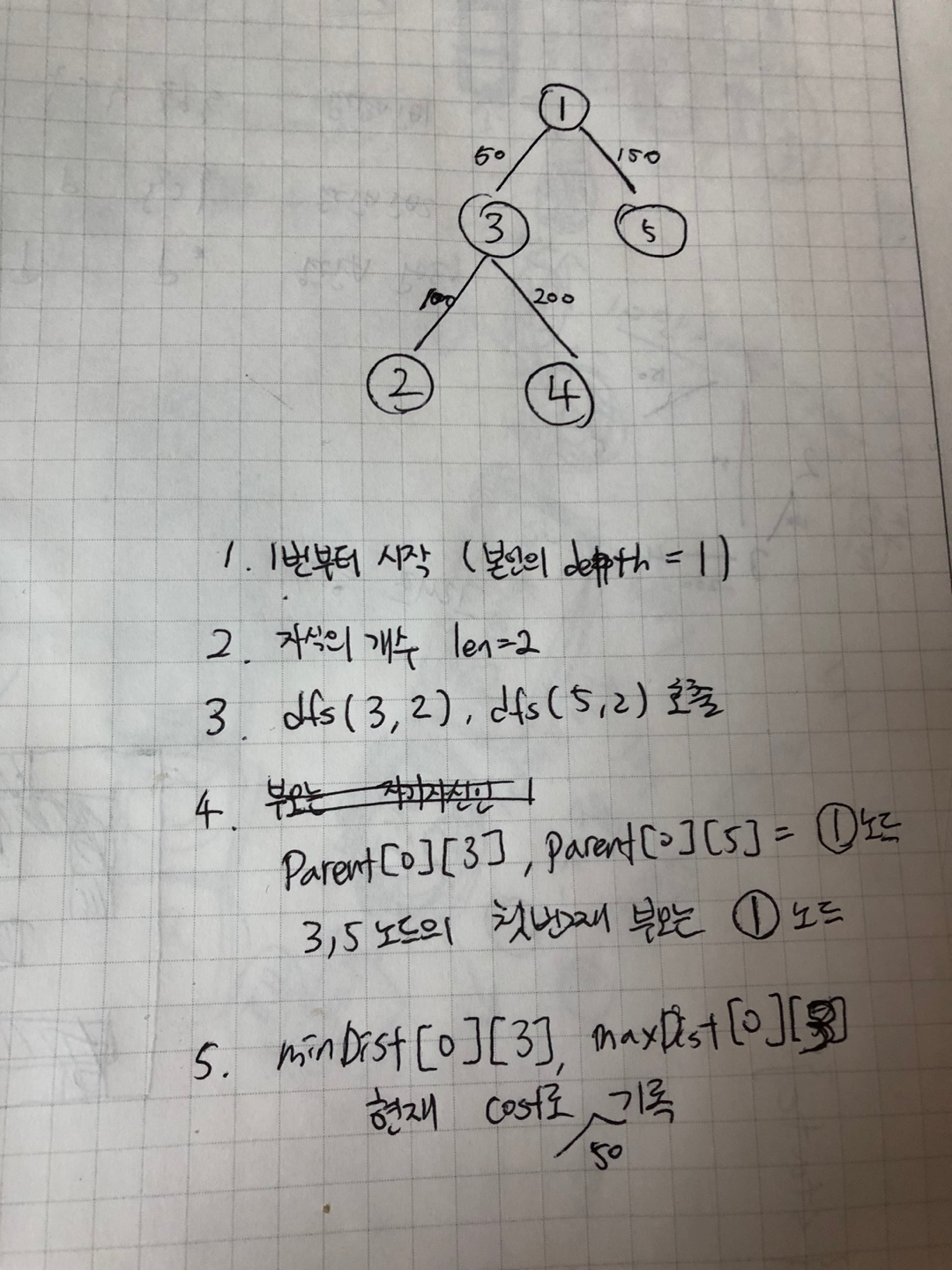
    }

3. 노드의 2^k번째 부모와 부모의 최대/최소 도로 길이의 dp배열을 갱신합니다.

 // 부모 채우기
    static void fillParent() {
        for (int i = 1; i<K; i++) {
            for (int j = 1; j<=N; j++) {
                parent[i][j] = parent[i-1][parent[i-1][j]];

                // 도로네트워크 추가
                minDist[i][j] = Math.min( minDist[i-1][j], minDist[i-1][parent[i-1][j]]);
                maxDist[i][j] = Math.max( maxDist[i-1][j], maxDist[i-1][parent[i-1][j]]);
            }
        }
    }

 

4. LCA를 통해 공통부모를 찾고 min, max를 찾습니다.

// 최소공통조상
    static void lca(int a, int b) {
        // 1. depth[a] >= depth[b] 이도록 조정하기
        if (depth[a] < depth[b]) {
            int tmp = a;
            a = b;
            b = tmp;
        }

        min = Integer.MAX_VALUE;
        max = -1;

        // 2. 더 깊은 a를 2^K승 점프하여 depth를 맞추기
        for (int i = K-1; i>=0; i--) {
            if (Math.pow(2, i) <= depth[a] - depth[b]) {
                min = Math.min(min, minDist[i][a]);
                max = Math.max(max, maxDist[i][a]);

                a = parent[i][a];
            }
        }

        // 3. depth를 맞췄는데 같다면 종료
        if (a == b) return;

        // 4. a-b는 같은 depth이므로 2^K승 점프하며 공통부모 바로 아래까지 올리기
        for (int i = K-1; i >= 0; i--) {
            if (parent[i][a] != parent[i][b]) {
                min = Math.min(min, Math.min(minDist[i][a], minDist[i][b]));
                max = Math.max(max, Math.max(maxDist[i][a], maxDist[i][b]));

                a = parent[i][a];
                b = parent[i][b];
            }
        }

        min = Math.min(min, Math.min(minDist[0][a], minDist[0][b]));
        max = Math.max(max, Math.max(maxDist[0][a], maxDist[0][b]));

        return;
    }

 

 

전체 코드

import java.io.*;
import java.util.*;

// 3176 도로 네트워크
public class Main_3176_도로네트워크 {

    static int N, K;	// N : 정점수, K : 2의 지수
    static int M;		// M : 쿼리 수 (문제에서 K)

    // LCA 관련 변수
    static int[] depth;
    static int[][] parent; // parent[K][V] 정점 V의 2^K번째 조상 정점 번호
    // parent[K][V] = parent[K-1][parent[K-1][V]];
    // TREE 변수
    static ArrayList[] tree;

    // 도로 네트워크 추가변수
    static int[][] minDist;	// minDist[K][V]  정점 V의 2^K번째 조상까지의 최소거리 도로
    static int[][] maxDist; // maxDist[K][V]  정점 V의 2^K번째 조상까지의 최대거리 도로

    static int min,max;

    static class edge{
        int target,cost;

        public edge(int target, int cost) {
            this.target = target;
            this.cost = cost;
        }
    }

    public static void main(String[] args) throws Exception {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        StringTokenizer st;

        // 1. 입력 & 변수 준비
        N = Integer.parseInt(br.readLine());

        // 2^K > N인 K 찾기
        K = 0;
        for (int i = 1; i <= N; i *= 2) {
            K++;
        }

        // LCA 관련 변수 초기화
        depth = new int[N + 1];
        parent = new int[K][N + 1];

        // 도로 네트워크 변수 초기화
        minDist = new int[K][N + 1];
        maxDist = new int[K][N + 1];

        // TREE 변수 초기화
        tree = new ArrayList[N+1];
        for (int i = 1; i <= N; i++) {
            tree[i] = new ArrayList<edge>();
        }

        int from,to,distance;
        for (int i = 1; i <= N-1; i++) {
            st = new StringTokenizer(br.readLine());
            from = Integer.parseInt(st.nextToken());
            to = Integer.parseInt(st.nextToken());
            distance = Integer.parseInt(st.nextToken());
            // 양방향 간선
            tree[from].add(new edge(to, distance));
            tree[to].add(new edge(from, distance));
        }

        // 2. DEPTH 확인
        dfs(1, 1);

        // 3. 2^N 까지 parent 채우기
        fillParent();

        // 4. LCA 진행
        M = Integer.parseInt(br.readLine());
        StringBuilder sb = new StringBuilder();
        for (int i=1; i<=M; i++) {
            st = new StringTokenizer(br.readLine());
            from = Integer.parseInt(st.nextToken());
            to = Integer.parseInt(st.nextToken());

            lca(from, to);
            sb.append(min+" "+max+"\n");
        }

        bw.write(sb.toString());

        bw.flush();
        bw.close();
        br.close();
    }

    // DEPTH 확인 DFS
    static void dfs(int id, int cnt) {
        // 1. depth를 기록
        depth[id] = cnt;

        // 2. 자식들의 depth를 기록
        int len = tree[id].size();
        for (int i = 0; i < len; i++) {
            edge next = (edge) tree[id].get(i);
            if (depth[next.target] != 0) {
                continue;
            }
            // 아직 깊이를 모르면 → 미방문 노드
            dfs(next.target, cnt+1);
            parent[0][next.target] = id;		// 첫번째 부모를 기록

            minDist[0][next.target] = next.cost; // 현재 cost로 갱신
            maxDist[0][next.target] = next.cost; // 현재 cost로 갱신
        }
        return;
    }

    // 부모 채우기
    static void fillParent() {
        for (int i = 1; i<K; i++) {
            for (int j = 1; j<=N; j++) {
                parent[i][j] = parent[i-1][parent[i-1][j]];

                // 도로네트워크 추가
                minDist[i][j] = Math.min( minDist[i-1][j], minDist[i-1][parent[i-1][j]]);
                maxDist[i][j] = Math.max( maxDist[i-1][j], maxDist[i-1][parent[i-1][j]]);
            }
        }
    }

    // 최소공통조상
    static void lca(int a, int b) {
        // 1. depth[a] >= depth[b] 이도록 조정하기
        if (depth[a] < depth[b]) {
            int tmp = a;
            a = b;
            b = tmp;
        }

        min = Integer.MAX_VALUE;
        max = -1;

        // 2. 더 깊은 a를 2^K승 점프하여 depth를 맞추기
        for (int i = K-1; i>=0; i--) {
            if (Math.pow(2, i) <= depth[a] - depth[b]) {
                min = Math.min(min, minDist[i][a]);
                max = Math.max(max, maxDist[i][a]);

                a = parent[i][a];
            }
        }

        // 3. depth를 맞췄는데 같다면 종료
        if (a == b) return;

        // 4. a-b는 같은 depth이므로 2^K승 점프하며 공통부모 바로 아래까지 올리기
        for (int i = K-1; i >= 0; i--) {
            if (parent[i][a] != parent[i][b]) {
                min = Math.min(min, Math.min(minDist[i][a], minDist[i][b]));
                max = Math.max(max, Math.max(maxDist[i][a], maxDist[i][b]));

                a = parent[i][a];
                b = parent[i][b];
            }
        }

        min = Math.min(min, Math.min(minDist[0][a], minDist[0][b]));
        max = Math.max(max, Math.max(maxDist[0][a], maxDist[0][b]));

        return;
    }
}

 

출처

https://devowen.com/274

백준 3176 / LCA 알고리즘, DP, DFS / JAVA

https://subbak2.tistory.com/60

[BOJ 백준] LCA 2(11438) Java

https://www.youtube.com/watch?v=O895NbxirM8