-
가장 빠르게 소수를 찾는 방법알고리즘/알고리즘 2022. 3. 26. 00:01
소수란?
자신보다 작은 두 개의 자연수를 곱하여 만들 수 없는, 1보다 큰 자연수입니다.
https://jm-park.github.io/algorithm/2018/08/06/Prime-Number(%EC%86%8C%EC%88%98)-%ED%8C%90%EB%B3%84%EB%B2%95-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98.html 방법 1: 가장 간단한 방법
N이 소수인지 판별하기 위해서는 2 ~ N-1까지 나누어서 하나라도 나누어 떨어지는가를 확인하는 방법이 있습니다.
이는 한개의 숫자에 대해 소수인지 파별하기 위해서는 O(N)의 시간 복잡도를 가지며 N개의 수에 대해서는 O(N^2)의 시간 복잡도를 가집니다.
방법 2 : 제곱근
만약 12에 대하여 소수를 판별하려고 합니다.
12의 약수는 1, 2, 3, 4, 6, 12를 가집니다.
가장 간단한 방법처럼 12를 2부터 N-1까지 나누어보려고 할 때 2* 6 = 6 * 2의 성질을 이용한 방법입니다. (xy = yx)
제곱근을 기준으로 제좁근까지 나누어 떨어지는지 여부를 조사하면 더 빠르게 소수 판별이 가능합니다.
시간 복잡도 : O(sqrt(n))
방법 3: 에라토스테네스의 체 - 대량의 소수 얻기
방법 2처럼 n에 대한 약수로 접근하는 것이 아니라, n의 배수를 기반으로 접근합니다.
에라토스테네스의 체를 사용하여 1~100까지의 수가 소수인지 판별해 보겠습니다.
먼저 1은 소수가 아니므로 제외합니다.

https://library-of-k.tistory.com/79 2부터 시작해서 소수를 찾으면서 합성수를 제거해 나갑니다.
2의 배수들은 모두 2를 약수로 가지므로 2의 배수들을 제외합니다.
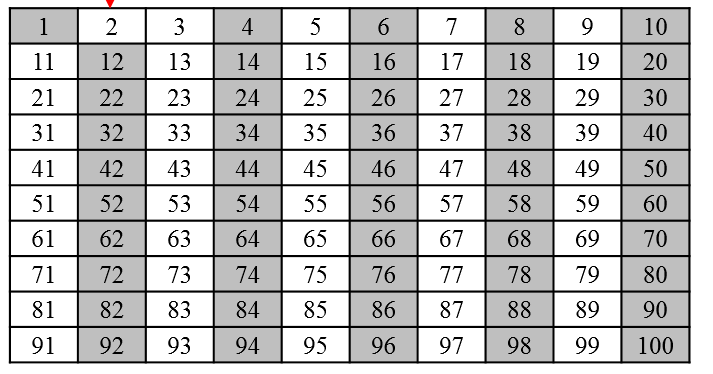
https://library-of-k.tistory.com/79 이제 다음으로 제외되지 않은 가장 작은 수 3을 선택하고, 3의 배수들을 제외합니다.
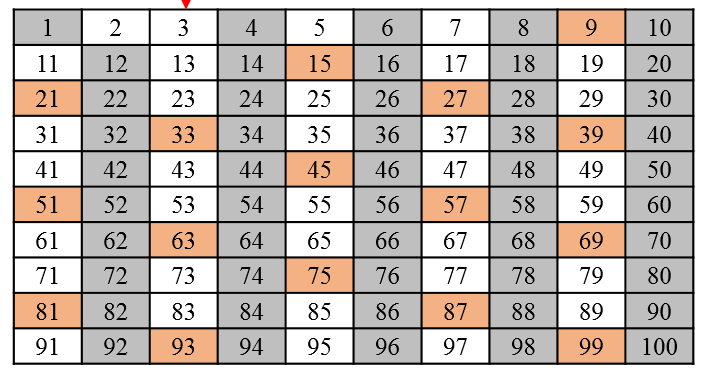
https://library-of-k.tistory.com/79 다음으로 제외되지 않은 가장 작은 수인 5를 선택하고, 5의 배수를 제외합니다.

https://library-of-k.tistory.com/79 다음으로 제외되지 않은 가장 작은 수인 7을 선택하고, 7의 배수를 제외합니다.
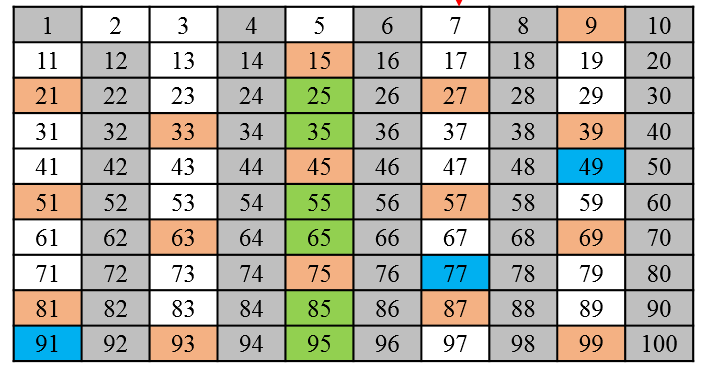
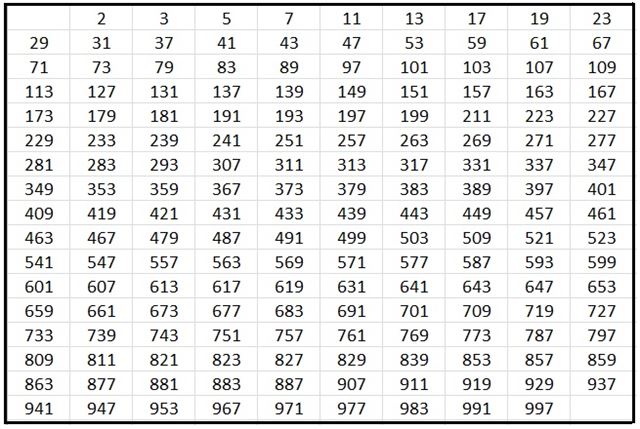
https://library-of-k.tistory.com/79 다음으로는 11, 13, 17 ~.... ~ 97 등의 수를 선택하여 배수를 제외하지만 배수가 존재하지 않습니다.
따라서 남아있는 하얀 수들이 소수가 됩니다.
시간복잡도 : O(NloglogN)
public class 에스토스테네스의체 { public static void main(String[] args) { // TODO Auto-generated method stub int targetNum = 100; boolean[] primeArray = new boolean[targetNum + 1]; for (int i = 2; i < targetNum; i++) { if (primeArray[i]) { continue; } for (int j = i*i; j < targetNum; j+=i) { if (primeArray[j]) continue; if (j % i == 0) { primeArray[j] = true; } } } for(int i=2; i<targetNum; i++) { if(primeArray[i]) { continue; } System.out.println(i); } } }출처
JM's IT Blog
개발쟁이가 되기 위한 생초짜의 기술 블로그 기록기
jm-park.github.io
https://library-of-k.tistory.com/79
효율적으로 소수 구하기 - 에라토스테네스의 체 (Sieve of Eratosthenes)
1. Introduction 소수는 1과 자기 자신외에는 약수를 가지지 않는 수를 의미한다. 소수를 판별하는 가장 간단한 방법은 2부터 자기자신까지의 수 (효율적으로는 $\sqrt {n}$까지)를 차례로 나눠보는 것
library-of-k.tistory.com
https://en.wikipedia.org/wiki/Sieve_of_Eratosthenes#Algorithm_complexity
Sieve of Eratosthenes - Wikipedia
From Wikipedia, the free encyclopedia Jump to navigation Jump to search Ancient algorithm for generating prime numbers Sieve of Eratosthenes: algorithm steps for primes below 121 (including optimization of starting from prime's square). In mathematics, the
en.wikipedia.org
'알고리즘 > 알고리즘' 카테고리의 다른 글
트라이 자료구조 (0) 2022.04.20 외판원 순회(TSP : Traveling Salesperson Problem) 알고리즘 (0) 2022.03.21 다익스트라(Dijkstra) 알고리즘 (0) 2022.03.17 세그먼트 트리란? (0) 2022.03.13 Upper_bound와 Lower_bound란? (0) 2022.03.10